TEORIA ESTATÍSTICA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI.

 TEORIA GRACELI DOS ESTADOS FÍSICOS, QUÂNTICO, E ESTADOS DE GRACELI.

ONDE OS ESTADOS FÍSICOS, QUÂNTICO, DE GRACELI VARIAM E SE TRANSFORMAM , E SE MANTÉM CONFORME O SISTEMA DIMENSIONAL CATEGORIAL GRACELI.

COM ISTO TAMBÉM SE TEM UMA  TEORIA GRACELI DIMENSIONAL CATEGORIAL.

SISTEMA DE VARIANTES FÍSICAS DE GRACELI [SDCTIE, TENSORES DE GRACELI E O INFINITO-DIMENSIONAL]. E CATEGORIAS FÍSICAS DE GRACELI.

ONDE ESTES SÃO AGENTES FUNDAMENTAIS REPRESENTADOS PELA MATÉRIA, ELEMENTOS QUÍMICOS, ESTRUTURA ELETRÔNICA DO ELEMENTOS, GRAUS ESPECÍFICOS DE VARIAÇÕES DE ENERGIAS E TRANSFORMAÇÕES EM INTERAÇÕES, E OUTROS.

SENDO AS CATEGORIAS FÍSICAS DE GRACELI [TIPO, NÍVEIS, POTECIAIS DE AÇÃO, TRANSFORMAÇÕES, INTERAÇÕES]  E OS ESTADOS FÍSICOS E ESTADOS DE GRACELI.

Distribuição de Fermi-Dirac em função de ε/μ para quatro temperaturas diferentes.

Em mecânica estatística, a estatística de Fermi-Dirac é uma estatística quântica que descreve o comportamento de sistemas de partículas com spin semi-inteiro, os férmions. Leva o nome de dois eminentes físicos: Enrico Fermi e Paul Adrien Maurice Dirac cada um dos quais descobriu o método de forma independente (embora Fermi tenha definido as estatísticas antes de Dirac).^[1][2] Antes do estudo da estatística de Fermi-Dirac é necessário compreender algumas diferenças entre sistemas clássicos e quânticos. Sistemas clássicos são formados, a priori, por partículas distinguíveis, ou seja, é possível identificar e diferenciar tais partículas individualmente e nestes sistemas os efeitos quânticos são desprezíveis, sendo o sistema descrito pela estatística de Maxwell–Boltzmann. Já sistemas quânticos são formados por partículas indistinguíveis, devido à superposição de suas funções de onda, ou seja é impossível descrevê-las individualmente e neste sistema os efeitos quânticos devem ser considerados. Sistemas quânticos podem ser descritos pelas estatísticas de Fermi-Dirac ou de Bose-Einstein, dependendo do spin das partículas.^[3][4]

• 5Referências

Formulação matemática

Como as partículas são indistinguíveis na estatística de Fermi-Dirac, a especificação do número de partículas é suficiente para determinarmos o estado do gás. Como os férmions obedecem ao princípio de exclusão de Pauli, não é possível que mais de uma partícula esteja no mesmo estado, se faz apenas necessário somar sobre todos os números possíveis de partículas em um único estado, ou seja, os dois possíveis valores ^[5]:

${\displaystyle n_{r}=0,1}$ para cada ${\displaystyle r}$

Quando o número total de partículas ${\displaystyle N}$ é fixado, a soma sobre todos os valores possíveis de ${\displaystyle n_{r}}$, com ${\displaystyle n_{1},n_{2},...}$ segue a seguinte relação

${\displaystyle \sum _{r}n_{r}=N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Dado um sistema com ${\displaystyle N}$ férmions em equilíbrio térmico a uma temperatura arbitrária ${\displaystyle T}$, o número médio de partículas ${\displaystyle <n_{s}>}$ em um estado particular ${\displaystyle s}$ com energia ${\displaystyle \epsilon _{s}}$ é obtido através da distribuição canônica, logo^[5]

${\displaystyle <n_{s}>={\frac {\sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}{\sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

no qual ${\displaystyle \beta ={\frac {1}{k_{B}T}}}$, sendo ${\displaystyle k_{B}}$ a constante de Boltzmann. Podemos renomear alguns termos na expressão acima, de forma que obtemos

${\displaystyle Z_{s}(N)=\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Somando sobre ${\displaystyle n_{s}}$ = 0 e 1, temos

${\displaystyle <n_{s}>={\frac {e^{-\beta \epsilon _{s}}Z_{s}(N-1)}{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

ou, ainda, podemos simplificar:

${\displaystyle <n_{s}>={\frac {1}{[Z_{s}(N)/Z_{s}(N-1)]e^{\beta \epsilon _{s}}+1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Na condição em que ${\displaystyle \Delta N\ll N}$, podemos escrever

${\displaystyle lnZ_{s}(N-\Delta N)=lnZ_{s}(N)-{\frac {\partial lnZ_{s}}{\partial N}}\Delta N=lnZ_{s}(N)-\alpha _{s}\Delta N}$

${\displaystyle Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

com ${\displaystyle \alpha _{s}={\frac {\partial lnZ_{s}}{\partial N}}}$. Como ${\displaystyle Z_{s}(N)}$ é uma soma sobre muitos estados, a variação de seu logaritmo com o número de partículas total ${\displaystyle N}$ não é afetado por qual estado particular ${\displaystyle s}$ foi omitido no somatório. Portanto, podemos fazer uma aproximação em que ${\displaystyle \alpha _{s}}$ é independente de ${\displaystyle s}$:

${\displaystyle \alpha _{s}=\alpha }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Ainda, podemos aproximar ${\displaystyle \alpha }$ em termos da derivada da função partição ${\displaystyle \mathrm {Z} (N)}$ sobre todos os estados, assim^[5]:

${\displaystyle \alpha ={\frac {\partial ln\mathrm {Z} }{\partial N}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Se utilizarmos ${\displaystyle \Delta N=1}$ na aproximação, encontraremos a distribuição de Fermi-Dirac^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\alpha +\beta \epsilon _{s}}+1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Ainda, o parâmetro ${\displaystyle \alpha }$ pode ser determinado pela primeira condição feita nesta dedução, em que

${\displaystyle \sum _{r}<n_{r}>=N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

ou

${\displaystyle \sum _{r}{\frac {1}{e^{\alpha +\beta \epsilon _{r}}+1}}=N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Da relação entre a função partição ${\displaystyle Z}$ e a energia livre de Helmholtz ${\displaystyle F}$, sabemos que ${\displaystyle F=-k_{B}Tln\mathrm {Z} }$, logo:

${\displaystyle \alpha =-{\frac {1}{k_{B}T}}{\frac {\partial F}{\partial N}}=-{\frac {\mu }{kT}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

${\displaystyle \alpha =-\beta \mu }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

onde ${\displaystyle \mu }$ é o potencial químico. Então outra forma de se definir a distribuição de Fermi-Dirac é^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}+1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Quando os níveis de energia são muito próximos, de modo que podemos considerar que formam um contínuo, o número médio de partículas com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$, pode ser escrito como^[5]

${\displaystyle n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Onde ${\displaystyle g(\epsilon )}$ é a densidade de estados, de modo que ${\displaystyle g(\epsilon )d\epsilon }$ fornece o número de estados com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$. E ${\displaystyle F(\epsilon )}$ é a chama função de Fermi, dada por^[5]

${\displaystyle F(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Interpretação física

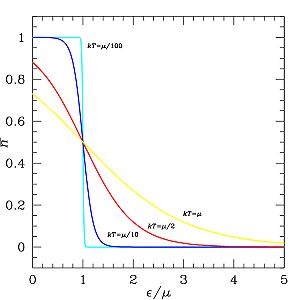
Para uma temperatura de 0 K, a função de Fermi é uma função de passo que vale 1 se ${\displaystyle \epsilon <\mu }$ e 0 se ${\displaystyle \epsilon >\mu }$. Ou seja, todos os estados com energia ${\displaystyle \epsilon <\mu }$ estão ocupados, enquanto os estados com energia ${\displaystyle \epsilon >\mu }$ estão vazios. A energia do último nível ocupado em 0 K se denomina energia de Fermi (${\displaystyle \epsilon _{F}}$) e corresponde ao potencial químico do sistema. Também é usual associar uma temperatura a esta energia mediante ${\displaystyle \epsilon _{F}=k_{B}T_{F}}$, sendo ${\displaystyle T_{F}}$ a temperatura de Fermi^[5].

No entanto, a definição mais precisa para a energia de Fermi é de que se trata da energia para a qual a função de Fermi é igual a 1/2, independentemente da temperatura. Deste modo, a energia de Fermi possui uma dependência com a temperatura embora muito fraca. Termodinamicamente, esta definição ainda equivale ao potencial químico do sistema^[6].

À medida que a temperatura do sistema aumenta, as partículas nos estados ligeiramente abaixo do nível de Fermi (até cerca de ${\displaystyle \epsilon _{F}-k_{B}T}$) são excitadas para estados com ${\displaystyle \epsilon >\epsilon _{F}}$ (até ${\displaystyle \epsilon _{F}+k_{B}T}$), e a função de Fermi deixa de ser uma função de passo e se apresenta mais suave, como pode ser visto na Figura 1. Estados com energias menor que ${\displaystyle \epsilon _{F}-k_{B}T}$ não são excitados em consequência do princípio de exclusão de Pauli, uma vez que a energia adquirida os levaria aos estados já ocupados^[5][6].

A distribuição de Fermi-Dirac tem importância capital no estudo de gases de férmions e em particular no estudo dos elétrons livres em um metal.

Aplicações

Conforme comentado anteriormente, as estatísticas de Fermi–Dirac e Bose–Einstein são aplicadas quando efeitos quânticos são apreciáveis e as partículas são consideradas "indistinguíveis". Os efeitos quânticos aparecem se a concentração de partículas (N/V) ≥ n_q (aonde n_q é a concentração quântica). A concentração quântica é atingida quando a distância média entre partículas é da ordem do comprimento de onda térmico de de Broglie, i.e. quando as funções de onda das partículas se superpõem^[3].

Em decorrência disto, as partículas se tornam indistinguíveis e os resultados obtidos para qualquer grandeza mensurável não pode depender da identificação da partícula. Como a concentração quântica depende da temperatura; altas temperaturas irão colocar a maioria dos sistemas no limite clássico, desde que não possuam uma densidade muito alta, e.g. uma anã branca.

A estatística de Fermi–Dirac é aplicada a férmions (partículas com spin semi-inteiro que obedecem ao princípio de exclusão de Pauli) uma vez que sistemas constituídos de férmions devem ser descritos por uma autofunção total antissimétrica, o que implica na impossibilidade da existência de duas ou mais partículas ocuparem o mesmo estado; enquanto a estatística de Bose–Einstein é aplicada a bósons (partículas com spin inteiro). Tanto Fermi–Dirac quanto Bose–Einstein tornam-se a estatística de Maxwell–Boltzmann em altas temperaturas ou baixas concentrações^[5].

A estatística de Maxwell–Boltzmann é frequentemente descrita como estatística de partículas clássicas "distinguíveis". Em outras palavras a configuração de partícula A no estado 1 e a partícula B no estado 2 é diferente do caso onde a partícula B está no estado 1 e a partícula A está no estado 2. Quando esta ideia é estendida, conduz à distribuição própria (de Boltzmann) de partículas em estados de energia, mas conduz a resultados sem significado físico para a entropia, conforme incorporado no paradoxo de Gibbs. Estes problemas desaparecem quando se percebe que todas as partículas são de fato indistinguíveis entre si, isto é, se levamos as estatísticas quânticas ao limite clássico obtemos os resultados corretos para entropia e outras grandezas termodinâmicas^[5].

A distribuição estatística de Maxwell–Boltzmann é particularmente útil para estudar gases ideais clássicos. A distribuição estatística de Fermi–Dirac é mais usualmente usada para o estudo do comportamento de elétrons em sólidos. Como tal, é a base da teoria dos dispositivos semicondutores e da eletrônica.

Aplicação em elétrons de condução em um metal

Uma aplicação comumente feita para a estatística de Fermi-Dirac se faz quando analisamos o comportamento de elétrons de condução em um metal. Isso é possível, pois, em um metal há muitos elétrons de condução cujas funções de onda se superpõem. O potencial gerado pelos íons positivos na rede cristalina se aproxima de um poço quadrado, de modo que é possível considerar o interior do sólido como uma região de potencial aproximadamente constante para esses elétrons com os limites do metal agindo como altas barreiras de potencial^[3]. A repulsão mútua entre os elétrons é muito próxima de zero, por causa disso podemos considerar os elétrons de condução como partículas livres, assim tratando como um gás de elétrons, portanto, sendo possível utilizar a descrição de Fermi-Dirac.

A densidade de estados calculada para este gás de elétrons contidos em um sólido de volume ${\displaystyle V}$ é^[6]

${\displaystyle g(\epsilon )d\epsilon ={\frac {8\pi V}{h^{_{3}}}}(2m^{_{3}})^{_{1/2}}\epsilon ^{_{1/2}}d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Logo,

${\displaystyle n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon ={\frac {8\pi V}{\hbar ^{3}}}(2m^{3})^{1/2}{\frac {\epsilon ^{1/2}d\epsilon }{e^{\frac {\epsilon -\epsilon _{F}}{k_{B}T}}+1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Com base nesta equação, encontramos a distribuição dos elétrons na banda de condução. Podemos calcular também uma relação para a energia de Fermi, fazendo ${\displaystyle T}$ = 0 e integrando a equação de 0 até ${\displaystyle \epsilon _{F}}$, temos que

${\displaystyle \int _{0}^{\epsilon _{F}}N(\epsilon )d\epsilon =N}$,

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

sendo ${\displaystyle N}$ o número total de elétrons. Portanto,

${\displaystyle {\frac {8\pi V}{\hbar ^{3}}}(2m^{3})^{1/2}\int _{0}^{\epsilon _{F}}\epsilon ^{_{1/2}}d\epsilon =N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

${\displaystyle \epsilon _{F,0}={\frac {h^{_{2}}}{8m}}\left({\frac {3N}{\pi V}}\right)^{_{2/3}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Onde o índice 0, indica que esta é a energia de Fermi para uma temperatura de zero absoluto. A pressão do gás de elétrons pode ser escrita como ${\displaystyle p={\frac {2N}{5V}}\epsilon _{F}}$ ^[7]

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Calor específico eletrônico

A partir da estatística de Fermi-Dirac, também é possível determinar a contribuição dos elétrons livres de um metal para o calor específico de um sólido. Uma análise detalhada mostra que o calor específico molar a volume constante devido aos elétrons é^[5]

${\displaystyle c_{V}={\frac {3R}{2}}\left({\frac {\pi ^{2}T}{3T_{F}}}\right)}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Como a temperatura de Fermi é muito elevada (cerca de 80000 K para o cobre), a contribuição dos elétrons livres para o calor específico é, em geral, desprezível, o que explica o fator do calor específico a volume constante de isolantes e condutores ser igual em condições típicas de temperatura.^[5]

Aplicação em estrelas anãs brancas

Outra aplicação importante trata-se dos gases de Fermi degenerados, relevantes na análise da constituição de uma estrela anã branca. O gás de elétrons descrito pela estatística de Fermi-Dirac se encontra tanto em metais, especialmente na condução, como também no interior de estrelas anãs brancas, que possuem densidades extremas e temperaturas também imensas, e a pressão do gás de elétrons no interior dessas estrelas impedem que as mesmas entrem em colapso. Os elétrons se encontram a uma energia cinética gigantesca ^[8] que assim consegue contrabalancear a gravidade, se isso não for suficiente ocorre o colapso em que elétrons se combinam nos prótons e, portanto, geram um nêutron. Isso pode acarretar em uma estrela de nêutron que possui ordens de densidade estratosféricas, no qual uma colher de chá de algo tão denso teria uma massa de 50 toneladas.

Termodinâmica
Processo de convecção.
Glossário de termodinâmica
Ramos[Esconder] Clássica Estatística Química
Leis[Expandir]
Sistema termodinâmico[Expandir]
Grandezas físicas[Expandir]
Propriedades[Expandir]
Equações termodinâmicas[Expandir]
Potencial termodinâmico[Expandir]
História Cultura [Expandir]
Cientistas[Expandir]
v d e

Em um sistema quântico constituído de muitas partículas idênticas com spin inteiro, a estatística de Bose-Einstein, ou estatística BE, é utilizada para descrever o sistema e calcular os valores médios das grandezas físicas.

Em um sistema de ${\displaystyle N}$ bósons idênticos de massa ${\displaystyle m}$, que possuem interação mútua desprezível, contidos em um recipiente de volume ${\displaystyle V}$, a uma temperatura ${\displaystyle T}$, em equilíbrio, o número médio de partículas ${\displaystyle {\bar {n}}_{s}}$ num estado de energia ${\displaystyle s}$ é dado por

${\displaystyle {\bar {n}}_{s}={\frac {g_{s}}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$ ,

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

em que ${\displaystyle g_{s}}$ é a degenerescência quântica do estado ${\displaystyle s}$, ${\displaystyle \epsilon _{s}}$ é a energia do estado ${\displaystyle s}$, ${\displaystyle \mu }$ é o potencial químico, e ${\displaystyle \beta =1/k_{B}T}$, em que ${\displaystyle k_{B}}$ é a constante de Boltzmann^[1].

Índice

• 1Formulação matemática
• 2Gás de fótons
  • 2.1Radiação de corpo negro
• 3Comparação entre as estatísticas
• 4Condensação de Bose-Einstein
  • 4.1Temperatura crítica para um gás ideal de bósons
  • 4.2Hélio líquido
• 5Referências
• 6Bibliografia

Formulação matemática

Seja um gás de ${\displaystyle N}$ partículas idênticas confinadas em um volume ${\displaystyle V}$. Sendo ${\displaystyle Q_{i}}$ o conjunto das coordenadas generalizadas da i-ésima partícula e ${\displaystyle s_{i}}$ o índice rotulador dos possíveis estados quânticos desta única partícula, o estado do gás inteiro é então descrito pelo conjunto de números quânticos

${\displaystyle \{s_{1},s_{2},\dots ,s_{N}\}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

os quais definem a função de onda ${\displaystyle \Psi }$ do gás nesse estado.

${\displaystyle \Psi =\Psi _{\{s_{1},s_{2},\dots ,s_{N}\}}(Q_{1},Q_{2},\dots ,Q_{N})}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A estatística BE trata de partículas em que o spin total é medido em unidade inteiras de ${\displaystyle \hbar }$ — os chamados bósons — como, por exemplo, o átomo de Hélio-4 e o fóton.^[1] Partículas quânticas são indistinguíveis, ou seja, a troca de duas partículas não altera o estado do sistema. Além disto, a função de onda total para um sistema de bósons é simétrica sobre a troca de duas partículas^[1]

${\displaystyle \Psi (\dots ,Q_{i},\dots ,Q_{j})=\Psi (\dots ,Q_{j},\dots ,Q_{i})}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Como consequência, os bósons não obedecem ao princípio de exclusão de Pauli, não havendo limitação no número de partículas que podem ocupar um dado estado quântico^[1]. Tomando este gás a uma temperatura ${\displaystyle T}$ e que cada partícula está em um estado ${\displaystyle r}$ de energia ${\displaystyle \epsilon _{r}}$ onde há ${\displaystyle n_{r}}$ partículas neste estado, o gás inteiro possui ${\displaystyle R}$ estados possíveis. Desprezando as interações mútuas entre as partículas, a energia do gás no estado ${\displaystyle R}$ será dada por

${\displaystyle E_{R}=n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\dots =\sum _{r}n_{r}\epsilon _{r}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

em que a soma se estende sobre todos os estados ${\displaystyle r}$ possíveis de uma partícula^[2]. Como o número de partículas é fixo, também temos que

${\displaystyle \sum _{r}n_{r}=N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A função partição ${\displaystyle Z}$ do gás será dada por

${\displaystyle Z=\sum _{R}e^{-\beta E_{R}}=\sum _{R}e^{-\beta n_{1}\epsilon _{1}+\dots }}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Essa soma é sobre todos os estados ${\displaystyle R}$ possíveis do gas inteiro, isto é, sobre todos os possíveis números ${\displaystyle n_{1},n_{2},n_{3},\dots }$^[2]. Como exp${\displaystyle [-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)]}$ é a probabilidade relativa de encontrar o gás em um estado partículas onde há ${\displaystyle n_{1}}$ partículas em 1, ${\displaystyle n_{2}}$ em partículas em 2 e assim sucessivamente, pode-se escrever o número médio de partículas em um estado ${\displaystyle s}$ como

${\displaystyle {\bar {n_{s}}}={\dfrac {\sum _{R}n_{s}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}{\sum _{R}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}}.}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Somando todos os possíveis valores de ${\displaystyle n_{s}}$, usando a propriedade multiplicativa da exponencial e rearranjando, pode-se escrever ${\displaystyle {\bar {n_{s}}}}$ como

${\displaystyle {\bar {n_{s}}}={\dfrac {\displaystyle \sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\cdot \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}{\displaystyle \sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\cdot \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

em que o sobrescrito ${\displaystyle (s)}$ no somatório indica a soma com exceção do estado ${\displaystyle s}$ em particular. Adotando a notação:

${\displaystyle \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}=Z_{s}(N)}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A restrição de ${\displaystyle N}$ fixo implica que se uma partícula está no estado ${\displaystyle s}$, a soma ${\displaystyle \sum ^{(s)}}$ se estende pelas ${\displaystyle N-1,N-2,\dots }$ partículas restantes que podem ser colocadas nos estados ${\displaystyle n_{r}=1,2,3,\dots }$. Ao executar explicitamente a soma sobre ${\displaystyle {\bar {n_{s}}}}$ ter-se-á^[3]

${\displaystyle {\bar {n_{s}}}={\dfrac {0+e^{-\beta \epsilon _{s}}Z_{s}(N-1)+2e^{-2\beta \epsilon _{s}}Z_{s}(N-2)+\dots }{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)+2e^{-2\beta \epsilon _{s}}Z_{s}(N-2)+\dots }}}$

Estabelecendo a seguinte relação entre ${\displaystyle Z_{s}(N-\Delta N)}$ e ${\displaystyle Z_{s}(N)}$ onde ${\displaystyle N>>\Delta N}$

${\displaystyle \ln {Z_{s}(N-\Delta N)}=\ln {Z_{s}(N)}-{\dfrac {\partial \ln {Z_{s}}}{\partial N}}\cdot \Delta N=\ln {Z_{s}}-\alpha _{s}\Delta N}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

em que

${\displaystyle \alpha _{s}={\dfrac {\partial \ln {Z_{s}}}{\partial N}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

e portanto,

${\displaystyle Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Mas como ${\displaystyle Z_{s}(N)}$ é uma soma sobre muitos estados, espera-se que a variação de seu logaritmo natural com o número total de partícula seja imperceptível para o qual um estado particular ${\displaystyle s}$ seja omitido da soma^[3]. Vamos introduzir a aproximação de que ${\displaystyle \alpha _{s}}$ é independente de ${\displaystyle s}$, então podemos só escrever ${\displaystyle \alpha _{s}=\alpha }$ para todo ${\displaystyle s}$^[3]. Logo,

${\displaystyle \alpha ={\frac {\partial \ln {Z}}{\partial N}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Do ensemble canônico, sabe-se que essa derivada parcial resulta em ${\displaystyle -\beta \mu }$, em que ${\displaystyle \mu }$ é o potencial químico do gás^[3]. Portanto,

${\displaystyle \alpha =-\beta \mu }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Substituindo estes resultados em ${\displaystyle {\bar {n_{s}}}}$ teremos

${\displaystyle {\bar {n_{s}}}={\dfrac {e^{-\beta (\epsilon _{s}-\mu )}Z_{s}(N)+2e^{-2\beta (\epsilon _{s}-\mu )}Z_{s}(N)+\dots }{Z_{s}(N)+e^{-\beta (\epsilon _{s}-\mu )}Z_{s}(N)+2e^{-2\beta (\epsilon _{s}-\mu )}Z_{s}(N)+\dots }}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Cancelando ${\displaystyle Z_{s}(N)}$ ter-se-á

${\displaystyle {\bar {n_{s}}}={\dfrac {e^{-\beta (\epsilon _{s}-\mu )}+2e^{-2\beta (\epsilon _{s}-\mu )}+\dots }{1+e^{-\beta (\epsilon _{s}-\mu )}+2e^{-2\beta (\epsilon _{s}-\mu )}+\dots }}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Que é uma série geométrica. Usando a função partição de acordo com^[3] isso resultará em

${\displaystyle {\bar {n_{s}}}={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Se o estado ${\displaystyle s}$ é degenerado com degenerescência ${\displaystyle g_{s}}$ então o número médio de partículas com energia ${\displaystyle \epsilon _{s}}$ é obtido multiplicando a expressão anterior por ${\displaystyle g_{s}}$. Finalmente,

${\displaystyle {\bar {n_{s}}}={\frac {g_{s}}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$

A estatística de Bose-Einstein reduz-se à estatística de Maxwell-Boltzmann para energias: ${\displaystyle (\epsilon _{s}-\mu )>>kT}$^[4][5].

Gás de fótons

Um caso especial da estatística de Bose-Einstein é o gás de fótons. Fótons possuem spin inteiro igual a 1, então desta forma são considerados bósons. O caso é especial devido ao fato de que se considerarmos vários fótons dentro de um recipiente com volume V, o número destes fótons não será constante, pois conforme estes fótons interagem com as paredes do recipiente estes são absorvidos ou emitidos. Desta forma, não podemos impor um vínculo ao número total de fótons no sistema. Neste caso, precisaremos realizar as somas sobre todos os possíveis números de partículas em cada estado, da forma^[6]:

${\displaystyle n_{r}=0,1,2,3,...}$ para todo r.

A função partição para o gás de fótons é dada por:

${\displaystyle Z=\sum _{R}e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+...)}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

No qual R são todos os estados possíveis do gás. Como não há vínculos agora para o número de partículas por estado, podemos utilizar as propriedades das funções exponenciais e reescrever a soma acima como:

${\displaystyle Z=\sum _{n_{1},n_{2},...}e^{-\beta n_{1}\varepsilon _{1}}e^{-\beta n_{2}\varepsilon _{2}}...}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Ou ainda:

${\displaystyle Z=\left(\sum _{n_{1}=0}^{\infty }e^{-\beta n_{1}\varepsilon _{1}}\right)\left(\sum _{n_{2}=0}^{^{\infty }}e^{-\beta n_{2}\varepsilon _{2}}\right)...}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Como não há restrição para o número de fótons, as somas acima são consideradas até um número muito grande de partículas por estado de energia, no qual matematicamente isto se traduz a realizarmos a soma até o infinito, embora fisicamente, estejamos carregando a soma até um número muito grande de partículas. Como estamos tratando de uma exponencial com argumento negativo, após um certo valor os termos serão desprezíveis, não tendo problemas com divergências. Se olharmos com cuidado para as somas dentro dos colchetes acima, percebe-se que podemos escrevê-las como abaixo:

${\displaystyle \sum _{n_{1}=0}^{\infty }e^{-\beta n_{1}\varepsilon _{1}}=1+e^{-\beta \varepsilon _{1}}+e^{-2\beta \varepsilon _{1}}+...=\left({\frac {1}{1-e^{-\beta \varepsilon _{1}}}}\right)}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Ou seja, cada termo é uma soma geométrica. Assim, podemos reescrever a função partição da seguinte forma:

${\displaystyle Z=\left({\frac {1}{1-e^{-\beta \varepsilon _{1}}}}\right)\left({\frac {1}{1-e^{-\beta \varepsilon _{2}}}}\right)...}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

E o logaritmo natural da função partição, que é o qual estamos interessados é dado por:

${\displaystyle \ln {Z}=-\sum _{r}\ln {(1-e^{-\beta \varepsilon _{r}})}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Nosso próximo objetivo agora é encontrar o número médio de partículas em um estado de energia ${\displaystyle \varepsilon _{s}}$. Tal resultado pode ser obtido através da expressão abaixo^[6]:

${\displaystyle {\bar {n_{s}}}=-{\frac {1}{\beta }}{\frac {\partial \ln {Z}}{\partial \varepsilon _{s}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Realizando a derivação do logaritmo natural da função partição, temos o resultado abaixo:

${\displaystyle {\bar {n_{s}}}={\frac {e^{-\beta \varepsilon _{s}}}{1-e^{-\beta \varepsilon _{s}}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

O resultado acima é este pois a única derivada que não é zero é o termo da soma no qual ${\displaystyle r=s}$. Podemos simplificar o resultado acima, multiplicando e dividindo a expressão acima pela exponencial com o mesmo argumento, porém positivo, e assim obtemos o importante resultado dado por:

${\displaystyle {\bar {n_{s}}}={\frac {1}{e^{\beta \varepsilon _{s}-1}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Este resultado é conhecido como a distribuição de Planck, e fornece o número médio de fótons em um determinado estado s. Uma das aplicações mais famosas do resultado acima é no problema da radiação de corpo negro.

Radiação de corpo negro

Ver artigo principal: Radiação de corpo negro

Radiância espectral em função da frequência

Todo corpo a uma temperatura ${\displaystyle T}$ emite radiação eletromagnética. A distribuição de Planck fornece o espectro de emissão para uma classe especifica de corpos, os chamados corpos negros, definidos como os corpos que absorvem toda a radiação incidente. Pode-se modelar um corpo negro como uma cavidade metálica com volume ${\displaystyle V}$, tal que haja apenas um pequeno orifício em uma de suas paredes. Logo, esta cavidade absorve toda a radiação que entra por ali, e radiação emitida pelo orifício que é oriunda das emissões a partir das superfícies internas da cavidade se comporta como se fosse um corpo negro.^[7]

Busca-se a chamada radiância espectral ${\displaystyle R_{T}(f)df}$, que fornece a potência irradiada por unidade de área com frequência entre ${\displaystyle f}$ e ${\displaystyle f+df}$ pelo corpo estudado a uma data temperatura. Através de uma análise física do problema, pode-se mostrar que a radiância espectral está diretamente ligada com a densidade de energia dentro da cavidade. A relação entre as duas grandezas é dada por:

${\displaystyle R_{T}(f)={\frac {c}{4}}u_{T}(f)}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Pode-se então obter a densidade de energia, e assim resolve-se o problema da mesma maneira. A densidade de energia pode ser obtida a partir da probabilidade de um nível com energia ${\displaystyle \varepsilon _{s}}$ estar ocupado por ${\displaystyle n_{s}}$ fótons, sendo assim se multiplicarmos este valor pelo número de médio fótons por unidade de volume naquele estado, teremos a densidade de energia dentro desta cavidade na forma:^[8]

${\displaystyle u_{T}(\varepsilon )={g(\varepsilon ){\bar {\varepsilon _{s}}}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Onde ${\displaystyle g(\varepsilon )}$ é a densidade de estados ou degenerescência. Como temos o número médio de fótons em um estado ${\displaystyle s}$, basta multiplicar este número pela energia do estado ${\displaystyle s}$, assim:

${\displaystyle {\bar {\varepsilon _{s}}}={\frac {\varepsilon _{s}}{e^{\beta \varepsilon _{s}}-1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Como os estados do sistema estão muito próximos um dos outros, por conta da cavidade ocupar um volume V macroscópico, podemos tratar as variáveis como sendo contínuas. O número de estados por unidade de volume dentro da cavidade com frequência entre ${\displaystyle f}$ e ${\displaystyle f+df}$ é dada por:^[9]

${\displaystyle g(f)df={\frac {8\pi }{c^{3}}}f^{2}df}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Sabemos que a energia e a frequência de um fóton estão ligado pela expressão de Planck ${\displaystyle E=hf}$, desta forma se fizermos a substituição sugerida, obtemos assim a expressão para a densidade de energia dentro de uma cavidade.

${\displaystyle u_{T}(f)={\frac {8\pi h}{c^{3}}}{\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

E a radiância espectral é dada diretamente por:

${\displaystyle R_{T}(f)={\frac {2\pi h}{c^{2}}}{\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Todo o caminho feito para o obtenção do resultado foi a partir da análise das propriedades quânticas e estatísticas de fótons dentro de um volume V, e em equilíbrio térmico a uma temperatura T. Pode-se chegar no mesmo resultado analisando a interação da radiação eletromagnética dentro do volume V com as paredes do recipiente^[10].

Comparação entre as estatísticas

Comparação das distribuições de Maxwell-Boltzmann (MB), Bose-Einstein (BE) e Fermi-Dirac (FD).

Influência do potencial químico na distribuição BE.

Influência da temperatura na distribuição de BE.

Nota-se que um sistema de bósons possui uma maior ocupação dos estados, devido aos efeitos quânticos de simetria da função de onda do sistema ^[11]. Nesta distribuição identifica-se que para o regime ${\displaystyle (\epsilon -\mu )/kT>>1}$ as distribuições quânticas de Bose-Einstein (BE) e Fermi-Dirac (FD) se aproximam da distribuição clássica de Maxwell-Boltzmann (MB), que representa o regime de baixas densidades e altas temperaturas, ou seja, o limite clássico ^[12].

Em diferentes valores do potencial químico, nota-se que os estados de menor energia (próximos ao estado fundamental) são os mais populados. Para baixas temperaturas as partículas se concentram nos estados de menor energia. No limite de temperatura tendendo a zero, todas as partículas vão para o estado fundamental (${\displaystyle s=1}$), logo, ${\displaystyle {\bar {n}}_{1}\approx N}$ enquanto ${\displaystyle {\bar {n}}_{s}\approx 0}$ para os demais estados ^[13]. Já para altas temperaturas, devido à energia térmica do sistema, as partículas tem maior probabilidade de atingir estados mais energéticos.

Condensação de Bose-Einstein

O condensado de Bose-Einstein é uma fase da matéria formada por bósons a uma temperatura muito próxima do zero absoluto. Nestas condições, uma grande fração de átomos atinge o mais baixo estado quântico, e nestas condições os efeitos quânticos podem ser observados em escala macroscópica. Sistemas em baixa temperatura ou com densidade relativamente alta de partículas são mais prováveis de apresentarem comportamentos quânticos, mesmo em sistemas onde a interação intramolecular é desprezível^[14].

Temperatura crítica para um gás ideal de bósons

Um gás ideal de bósons não está sujeito ao princípio de exclusão de Pauli. Logo, os bósons podem se condensar no seu estado de menor energia. A densidade de estados ${\displaystyle g(\epsilon )}$ é dada por,

${\displaystyle g(\epsilon )={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\epsilon ^{1/2}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Logo, o número de partículas ${\displaystyle N}$ pode ser reescrito como

${\displaystyle N=\int _{0}^{\infty }{\frac {g(\epsilon )}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A distribuição continua pode ser utilizada pois os níveis do sistema quântico discreto são numerosos e estão muito próximos. Portanto,

${\displaystyle N={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Porém, como a integração dar-se-á de ${\displaystyle \epsilon =0}$, a informação do estado fundamental é perdida. Todavia, quando a temperatura do sistema diminui, o potencial químico aumenta, e o número de partículas no estado fundamental é dada por ^[15]

${\displaystyle N_{0}={\frac {1}{e^{-\beta \mu }-1}}}$

Seja o número de partículas em estados excitados dado por ${\displaystyle N_{e}}$, temos

${\displaystyle N=N_{0}+N_{e}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

${\displaystyle N={\frac {1}{e^{-\beta \mu }-1}}+{\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

Porém, para temperaturas muito próximas de zero ${\displaystyle N\approx N_{0}}$, ou seja,

${\displaystyle N\approx {\frac {1}{e^{-{\frac {\mu }{kT}}}-1}}}$

Variação da temperatura de No/N (preto) e de Ne/N (vermelho) para uma gás ideal de bósons.

E, considerando ${\displaystyle N}$ grande,

${\displaystyle -{\frac {\mu }{kT}}\approx \ln \left(1+{\frac {1}{N}}\right)\approx {\frac {1}{N}}}$

Logo, ${\displaystyle e^{-\mu /kT}\approx 1}$. E ${\displaystyle N_{e}}$ se torna,

${\displaystyle N_{e}={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta \epsilon }-1}}d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Introduzindo a mudança de variável ${\displaystyle x=\beta \epsilon }$, temos

${\displaystyle N_{e}={\frac {2}{\sqrt {\pi }}}\left({\frac {2\pi mkT}{h^{2}}}\right)^{3/2}V\int _{0}^{\infty }{\frac {x^{1/2}}{e^{x}-1}}d\epsilon }$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A integral pode ser escrita em termos da função gama ${\displaystyle \Gamma (x)}$ e da função zeta de Riemann ${\displaystyle \zeta (x)}$. De fato, ela é igual a ${\displaystyle \Gamma (3/2)\zeta (3/2)}$, onde ${\displaystyle \Gamma (3/2)={\sqrt {\pi }}/2}$, logo,

${\displaystyle N_{e}=\zeta (3/2)V\left({\frac {2\pi mkT}{h^{2}}}\right)^{3/2}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

A temperatura crítica, ou de Bose-Einstein, ${\displaystyle T_{c}}$, é a temperatura em que acima dela todos os bósons estão em um estado excitado, e pode ser encontrada tomando ${\displaystyle N=N_{e}}$, onde ${\displaystyle T=T_{c}}$, assim, da última equação,

${\displaystyle T_{c}={\frac {h^{2}}{2\pi mk}}\left[{\frac {N}{\zeta (3/2)V}}\right]^{2/3}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Se ${\displaystyle 0<T<T_{c}}$, a razão de bósons no estado excitado em relação ao total, é

${\displaystyle {\frac {N_{e}}{N}}=\left({\frac {T}{T_{c}}}\right)^{3/2}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Consequentemente, a razão para os bósons no estado fundamental é,

${\displaystyle {\frac {N_{0}}{N}}=1-\left({\frac {T}{T_{c}}}\right)^{3/2}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Estatística de Maxwell–Boltzmann

Origem: Wikipédia, a enciclopédia livre.

Em mecânica estatística, a estatística Maxwell–Boltzmann descreve a distribuição estatística de partículas materiais em vários estados de energia em equilíbrio térmico, quando a temperatura é alta o suficiente e a densidade é baixa suficiente para tornar os efeitos quânticos negligenciáveis. A estatística Maxwell–Boltzmann é consequentemente aplicável a quase qualquer fenômeno terrestre para os quais a temperatura está acima de poucas dezenas de kelvins.^[1][2]

O número esperado de partículas com energia ${\displaystyle \epsilon _{i}}$ para a estatística de Maxwell–Boltzmann é ${\displaystyle N_{i}}$ onde:

${\displaystyle {\frac {N_{i}}{N}}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}}}={\frac {g_{i}e^{-\epsilon _{i}/kT}}{Z}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

onde:

• ${\displaystyle N_{i}}$ é o número de partículas no estado i
• ${\displaystyle \epsilon _{i}}$ é a energia do estado i-ésimo
• ${\displaystyle g_{i}}$ é a degenerescência do nível de energia i, o número de estados dos partículas (excluindo o estado de "partícula livre") com energia ${\displaystyle \epsilon _{i}}$
• ${\displaystyle \mu }$ é o potencial químico
• ${\displaystyle k}$ é a constante de Boltzmann
• ${\displaystyle T}$ é a temperatura absoluta
• ${\displaystyle N}$ é o número total de partículas

${\displaystyle N=\sum _{i}N_{i}\,}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

• ${\displaystyle Z}$ é a função partição

${\displaystyle Z=\sum _{i}g_{i}e^{-\epsilon _{i}/kT}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

• ${\displaystyle e^{(...)}}$ é a função exponencial, sendo e o número de Euler

A distribuição de Maxwell-Boltzmann tem sido aplicada especialmente à teoria cinética dos gases, e outros sistemas físicos, além de em econofísica para predizer a distribuição da renda. Na realidade a distribuição de Maxwell-Boltzmann é aplicável a qualquer sistema formado por N "partículas" ou "indivíduos" que interacambiam estacionariamente entre si uma certa magnitude ${\displaystyle m}$ e cada um deles têm uma quantidade ${\displaystyle m_{i}}$ da magnitude ${\displaystyle m}$ e ao longo do tempo ocorre que ${\displaystyle \sum _{i=1}^{N}M=m_{1}+m_{2}+...+m_{N}}$.

Limites de aplicação

Para um sistema de partículas quânticas, a hipótese de que ${\displaystyle N_{i}}$ seja substancialmente menor que ${\displaystyle g_{i}}$ para os estados diferentes do fundamental em geral não se cumprirá e é necessário recorrer-se à estatística de Bose-Einstein se as partículas são bosônicas ou à estatística de Fermi-Dirac se as partículas são fermiônicas.

As estatísticas de Bose–Einstein e Fermi–Dirac podem ser expressas como:

${\displaystyle N_{i}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}\pm 1}}}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Assumindo que o valor mínimo de ${\displaystyle \epsilon _{i}}$ é bastante pequeno, se pode verificar que a condição na qual a distribuição de Maxwell-Boltzmann é válida é quando se cumpre que:

${\displaystyle e^{-\mu /kT}\gg 1}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

Para um gás ideal, podemos calcular os potenciais químicos utilizando o desenvolvimento da equação de Sackur–Tetrode para demonstrar que:

${\displaystyle \mu =\left({\frac {\partial E}{\partial N}}\right)_{S,V}=-kT\ln \left({\frac {V}{N\Lambda ^{3}}}\right)}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

onde ${\displaystyle E}$ é a energia interna total, ${\displaystyle S}$ é a entropia, ${\displaystyle V}$ é o volume, e ${\displaystyle \Lambda }$ é o comprimento de onda térmico de de Broglie. A condição de aplicação para a distribuição Maxwell-Boltzmann em um gás ideal resulta:

${\displaystyle {\frac {V}{N\Lambda ^{3}}}\gg 1.}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

O princípio de exclusão de Pauli é um princípio da mecânica quântica formulado por Wolfgang Pauli em 1925. Ele afirma que dois férmions idênticos não podem ocupar o mesmo estado quântico simultaneamente. Uma forma mais rigorosa de enunciar este princípio é dizer que a função de onda total de um sistema composto por dois férmions idênticos deve ser antissimétrica, com respeito ao cambiamento de duas partículas. Para elétrons de um mesmo átomo, ele implica que dois elétrons não podem ter os mesmos quatro números quânticos. Por exemplo, se os números quânticos ${\displaystyle n}$, ${\displaystyle l}$, e ${\displaystyle m_{l}}$ são iguais nos dois elétrons, estes deverão necessariamente ter os números ${\displaystyle m_{s}}$ diferentes, e portanto os dois elétrons têm spins opostos.

O princípio de exclusão de Pauli é uma consequência matemática das restrições impostas por razões de simetria ao resultado da aplicação do operador de rotação a duas partículas idênticas de spin semi-inteiro.

Índice

• 1Sumário
• 2História
• 3Conexão com a simetria do estado quântico
• 4Consequências
• 5Ver também
• 6Referências
• 7Bibliografia
• 8Ligações externas

Sumário

O princípio de exclusão de Pauli é um dos mais relevantes princípios da física, basicamente porque os três tipos de partículas que formam a matéria ordinária - elétrons, prótons e nêutrons - têm que satisfazê-lo. O princípio de exclusão de Pauli é a razão fundamental para muitas das propriedades características da matéria, desde sua estabilidade até a existência das regularidades expressas pela tabela periódica dos elementos.

O princípio de exclusão de Pauli é uma consequência matemática das propriedades do operador momento angular, que é o gerador das operações de rotação, em mecânica quântica. A permutação de partículas num sistema de duas partículas idênticas (que é matematicamente equivalente à rotação de cada partícula de um ângulo de 180 graus) deve resultar em uma configuração descrita pela mesma função de onda da configuração original (quando as partículas têm spin inteiro) ou numa mudança de sinal desta função de onda (para partículas de spin semi-inteiro). Por isso, duas partículas de spin semi-inteiro não podem estar em um mesmo estado quântico, já que a função de onda do sistema composto pelas duas teria que ser igual a sua simétrica, e a única função que atende a esta condição é a função identicamente nula.

Partículas com função de onda anti-simétrica são chamadas férmions, e obedecem ao princípio de exclusão de Pauli. Além das mais familiares já citadas - elétron, próton e nêutron - são também fermions o neutrino e o quark (que são os constituintes elementares dos prótons e nêutrons), além de alguns átomos, como o hélio-3. Todos os férmions possuem spin "semi-inteiro", o que quer dizer que seu momento angular intrínseco tem valor ${\displaystyle \hbar ={\frac {h}{2\pi }}}$ 

Um sistema formado por partículas idênticas com spin inteiro é descrito por uma função de onda simétrica; estas partículas são chamadas bósons. Ao contrário dos fermions, elas podem partilhar um mesmo estado quântico. São exemplos de bósons o fóton e os bósons W e Z.

História

No início do século XX tornou-se evidente que átomos e moléculas com elétrons emparelhados ou um número par de eletrons são mais estáveis que aqueles com um número ímpar de eletrons. Num artigo publicado em 1916 por Gilbert N. Lewis^[1], por exemplo, a regra três dos seis postulados propostos pelo autor para explicar o comportamento químico das substâncias estabelece que um átomo tende a ter um número par de elétrons em sua camada de valência, sendo esse número, de preferência oito, que estão normalmente dispostos simetricamente nos oito vértices de um cubo (ver: átomo cúbico). Em 1922 Niels Bohr mostrou que a tabela periódica pode ser explicada pela hipótese de que certos números de elétrons (por exemplo, 2, 8 e 18) correspondem a "camadas fechadas" estáveis.

Pauli procurou uma explicação para estes números, que eram a esta altura apenas empíricos. Ao mesmo tempo, ele estava tentando explicar certos resultados experimentais envolvendo o Efeito Zeeman em espectroscopia atômica e no ferromagnetismo. Ele encontrou uma pista essencial em um artigo de 1924 escrito por E.C.Stoner, que estabelecia que, para um dado valor do número quântico principal (${\displaystyle n}$), o número de níveis de energia de um eletron no espectro de um átomo de metal alcalino posto sob a ação de um campo magnético externo, situação na qual todos os níveis de energia degenerados são separados, é igual ao número de elétrons na camada fechada de um gás nobre correspondente ao mesmo valor de ${\displaystyle n}$. Este fato levou Pauli a perceber que os números aparentemente complicados de elétrons em camadas fechadas podem ser reduzidos a uma regra muito simples, a de que só pode haver um elétron em cada estado atômico, definido por um conjunto de quatro números quânticos. Para esta finalidade ele introduziu um novo número quântico com apenas dois valores possíveis, identificado por Samuel Goudsmit e George Uhlenbeck como o spin do eletron.

Conexão com a simetria do estado quântico

O princípio de exclusão de Pauli pode ser deduzido a partir da hipótese de que um sistema de partículas só pode ocupar estados quânticos anti-simétricos. De acordo com o teorema spin-estatística, sistemas de partículas idênticas de spin inteiro ocupam estados simétricos, enquanto sistemas de partículas de spin semi-inteiro ocupam estados anti-simétricos; além disso, apenas valores de spin inteiros ou semi-inteiros são permitidos pelos princípio da mecânica quântica.

Como discutido no artigo sobre partículas idênticas, um estado anti-simétrico no qual uma das partículas está no estado ${\displaystyle \left|\psi _{1}\right\rangle }$ (nota) enquanto a outra está no estado ${\displaystyle \left|\psi _{2}\right\rangle }$ é

${\displaystyle |\psi _{1},\psi _{2}\rangle ={\frac {1}{\sqrt {2}}}{\Big (}|\psi _{1}\rangle |\psi _{2}\rangle -|\psi _{2}\rangle |\psi _{1}\rangle {\Big )}.}$

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

No entanto, se ${\displaystyle \left|\psi _{1}\right\rangle }$ e ${\displaystyle \left|\psi _{2}\right\rangle }$ são exatamente o mesmo estado, a expressão acima é identicamente nula:

${\displaystyle |\psi _{1},\psi _{2}\rangle =0.}$

Isto não representa um estado quântico válido, porque vetores de estado que representem estados quânticos têm obrigatoriamente que ser normalizáveis, isto é devem ter norma finita. Em outras palavras, nunca poderemos encontrar as partículas que formam o sistema ocupando um mesmo estado quântico.

X

SISTEMA DO INFINITO-DIMENSIONAL CATEGORIAL GRACELI 

(a constante de Planck dividida por ${\displaystyle 2\pi }$) multiplicada por um semi-inteiro (${\displaystyle {\frac {1}{2}}}$, ${\displaystyle {\frac {3}{2}}}$, ${\displaystyle {\frac {5}{2}}}$, etc.). Na teoria da mecânica quântica, fermions são descritos por "estados anti-simétricos", que são explicados em mais detalhes no artigo sobre partículas idênticas.